Topological sort

Topological sort is an algorithm that, given a directed acyclic graph with \(n\) vertices and \(m\) edges, a topological sort gives the vertices in an order such that, if there is an edge from vertex \(v\) to vertex \(u\), then \(v\) must appear before \(u\). Here is an example:

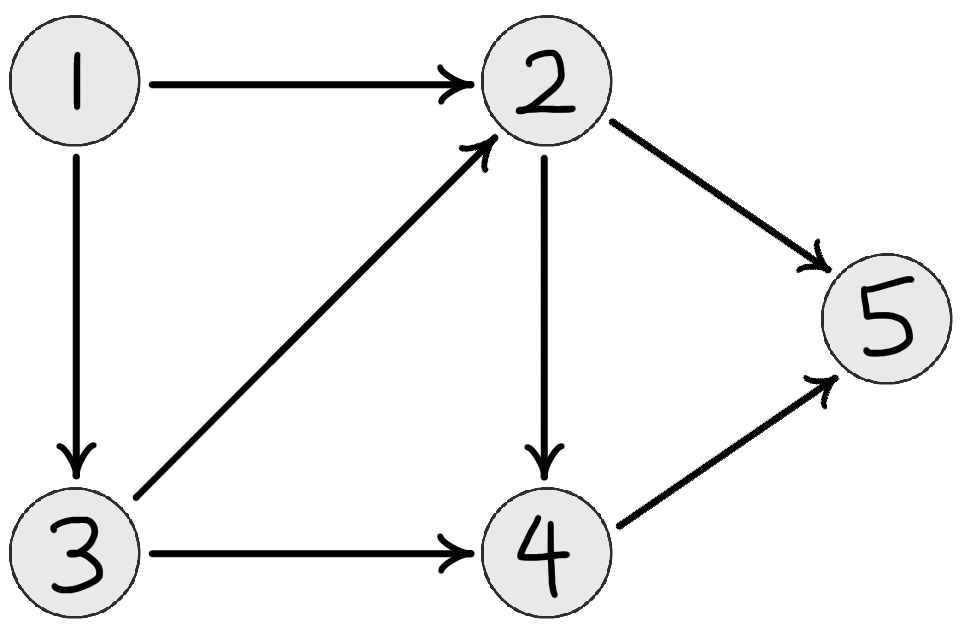
Here, as \(1\) is the only node with no edges connected to it, it will be first. It is connected to vertices \(2\) and \(3\), but vertex \(3\) is also connected to \(2\), meaning that \(3\) goes before \(2\), giving \(1 3 2\). Next is \(4\), as \(2\) and \(3\) both connect to \(4\), and last is \(5\), as \(4\) is connected to \(5\). Therefore, our topological sort should return \(1 3 2 4 5\).

Note why the graph needs to be acyclic for a sorting to exist. If there was a cycle, no node within is able to be sorted as there is always another pointing to it.

And another thing: does a sorting necessarily have to be unique? If not, can you give a counterexample? The solution will be shown later.

Implementation – Method 1

Let’s go back to our example and see how we did it, but in a slightly different way. Each time we choose a node, let’s remove it and all edges it has, giving this insightful diagram:

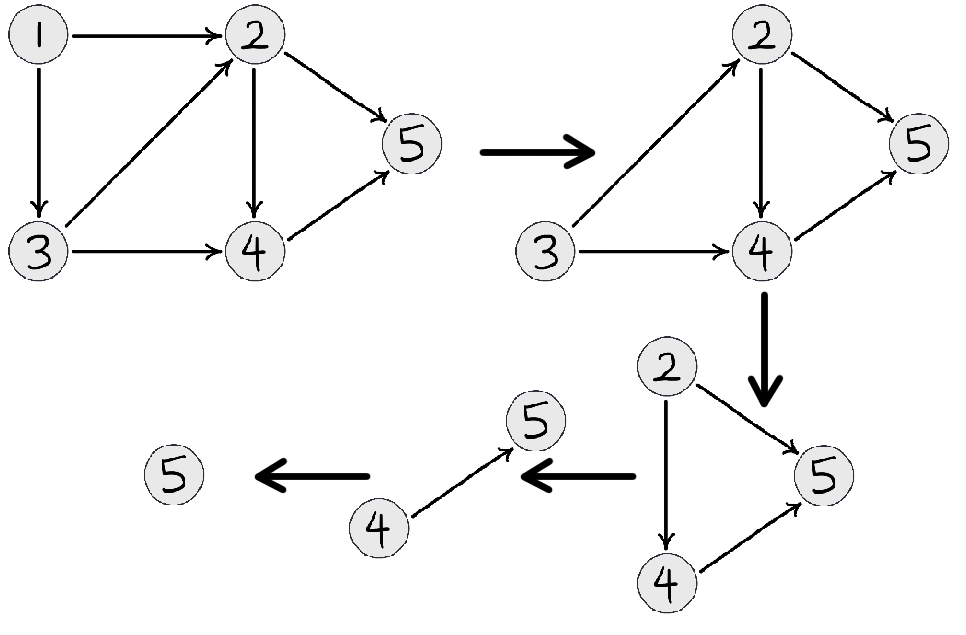
It looks like the next node to be sorted will always be the node with degree zero. Well, if you think about it, it’s kind of obvious, otherwise some other node would exist that needed to be sorted first, but this is the key of the algorithm. We simply can have an array deg[] that stores the degree of each node(the number of edges pointing to it). Topological sort can use two graph traversal algorithms: Depth-first search(DFS) and Breadth-first search(BFS). For this algorithm I use BFS as if the graph is large DFS can sometimes result in stack overflow. If a node has degree zero, we simply output that node, and remove all edges pointing away from it. If one of these removals results in another node having a degree of zero, we push that into the queue. Here is some C++ code that illustrates this algorithm:

#include <iostream>
#include <queue>
using namespace std;
int n, m, u, v, deg[100001], cnt;
vector<int> graph[100001];
queue<int> q;
int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> u >> v;
        graph[u].push_back(v);
        deg[v]++;
    }
    for (int i = 1; i <= n; i++) 
        if (deg[i] == 0) q.push(i); 
    while (!q.empty()) {
        int cur = q.front();
        q.pop();
        cout << cur << ' ';
        for (int i : graph[cur]) {
            deg[i]--;
            if (!deg[i]) q.push(i);
        }
    }
    return 0;
}

As you can see, the time complexity of this is \(O(n + m)\).

Now here is the answer to the problem I gave earlier. Topological sorting is not necessarily unique, for example you could have a graph with \(3\) vertices and directed edges \(1\rightarrow 2\) and \(1\rightarrow 3\). Therefore, if we want to find the ‘smallest’ sorting, C++’s std::set data structure is a natural candidate, as it automatically sorts its contents. It also allows me to seamlessly transition to the DFS approach (also \(O(n + m)\))!

Method 2

#include <iostream> 
#include <set>
using namespace std;
int n, m, u, v, deg[200001], start;
set<int> graph[200001];
void dfs (int cur) {
    cout << cur << ' ';
    for (int i : graph[cur]) {
        deg[i]--;
        if (!deg[i]) dfs(i);
    }
}
int main() {
    cin >> n >> m;
    for (int i = 1; 1 <= m; i++) {
        cin >> u >> v;
        graph[u].insert(v);
        deg[v]++;
    }
    for (int i = 1; i <= n; i++) 
        if (!deg [i]) {
            start = i;
            break;
        }
    dfs(start);
    return 0;
}

The end, now go practice!

That’s right, go try using and refining your new knowledge by doing problems! Now! Starting with E – Find Permutation (atcoder.jp)!