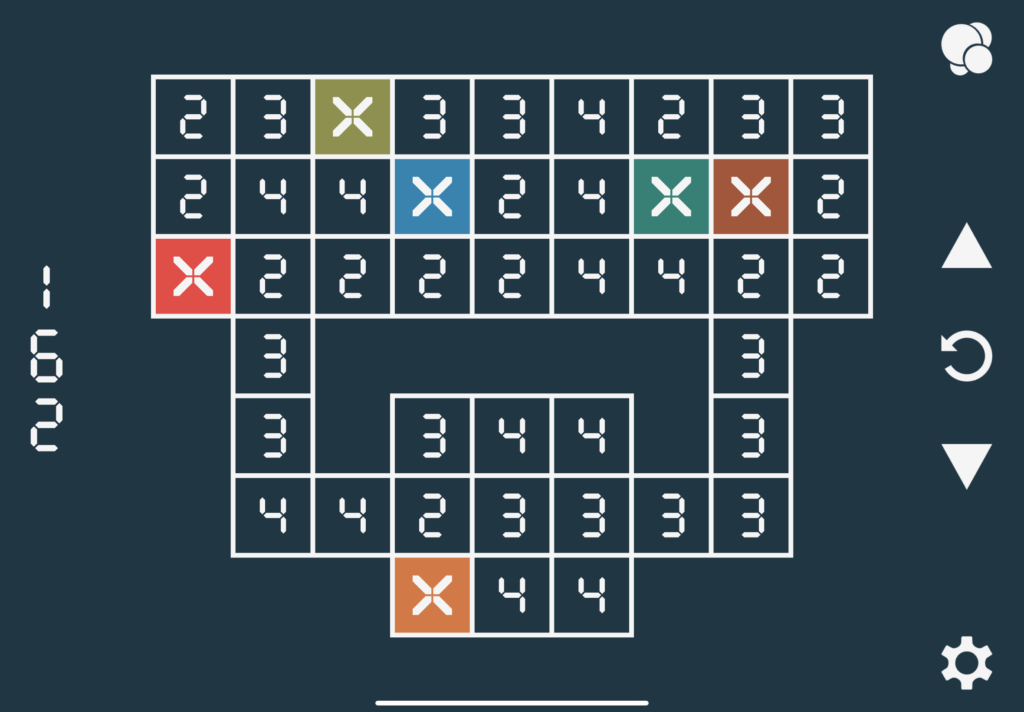
Cardinal Chains is a pretty little minimalist puzzle game that I downloaded a few years ago. With the small price of 3 dollars gives you 500 challenging levels to work through (I’m around the 350s at the time of writing). Within each level is some arrangement of square cells in a grid. Each cell either has a positive integer or an ‘X’ in it. From these ‘X’s, you must create nonintersecting paths to fill the entire map, and the sequence of numbers in a path starting from the ‘X’ must be non-decreasing, hence the name. Here’s an example of a level.

There’s a free online version with the first 100 levels: Cardinal Chains by Daniel Nora (itch.io)
First Program
Yesterday I was stuck on level 333.

After some fiddling about, I was completely lost with no idea how to do this level. So I did what a programmer does best: write a program (what else?) to do it for me. Thankfully, this was a pretty basic implementation Breadth-First Search which I got done in around 10 minutes. First, I represented the grid as a 2D integer array, where normal cells were the number they contained, blank cells -1, and the ‘X’ 0. Then I just defined some other constants like the size of the grid and the arrays to change the coordinates.
const int n = 6, m = 7, sz = 38;
int grid[n][m] = {
{3, -1, 3, 3, 3, 3, -1},
{3, 3, 3, 3, 3, 3, 0},
{3, 3, 3, 3, 3, 3, -1},
{3, 3, 3, 3, 3, 3, 3},
{3, 3, 3, 3, 3, 3, 3},
{-1, 3, 3, 3, 3, 3, 3}
};
const int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};Then, I defined the path as a struct containing it’s length and a vector of coordinates.
struct path {
int sz;
vector<pair<int, int> > v;
};After that the BFS was quite straightforward.
int main() {
queue<path> q;
path init;
init.sz = 1, init.v.push_back(make_pair(1, 6));
q.push(init);
while (!q.empty()) {
path cur = q.front();
q.pop();
if (cur.sz == sz) {
for (pair<int, int> i : cur.v)
cout << i.first << ' ' << i.second << endl;
return 0;
}
pair<int, int> pos = cur.v.back();
for (int i = 0; i < 4; i++) {
int nx = pos.first + dx[i], ny = pos.second + dy[i];
pair<int, int> npos = make_pair(nx, ny);
if (nx < 0 || ny < 0 || nx >= n || ny >= m) continue;
if (grid[nx][ny] == -1) continue;
bool flag = true;
for (pair<int, int> j : cur.v) if (j == npos) flag = false;
if (!flag) continue;
path nw = cur;
nw.v.push_back(npos), nw.sz++;
q.push(nw);
}
}
cout << "impossible";
return 0;
}Of course this was wildly inefficient, taking nearly a full minute to solve. But it got the job done, and I moved on to the next level.
The Extension
Although difficult, this level was hardly anything in terms of complexity. All numbers were the same, and there was only one starting point. If I wanted to truly defeat this game, I needed to write a better program. To start, I made a small modification to make the numbers in the path non-decreasing. If you look at line 23 of the main function above, a new path is disallowed if the new cell is a wall or a starting point. So, we can modify it as follows:
if (grid[nx][ny] == -1) continue;
// becomes
if (grid[nx][ny] < grid[pos.first][pos.second]) continue;
// where pos was defined as the ending cell in the path
pair<int, int> pos = cur.v.back();I also changed up the path struct so that the vector was called coords instead of v for readability. Now I set my focus on having multiple paths. My initial idea was to store all the possible paths for each starting point, then DFS through them. As the size of the map wasn’t ridiculously big and nearly always under 50, the numbers wouldn’t be too big, and the program would hopefully finish in under a minute.
To try this, I first defined a new array start[k][2] (remember k is the number of starting points) to store the coordinates of all starting points. I then moved the BFS into its own function which took an argument x which told the function which starting point it would calculate on. Here I encountered a slight issue: if two starting points were adjacent, then the function would think that it could draw a path into another starting point. Of course this is not allowed, so to police this case I set all starting points to -1, just like blank cells. Then, the function would set only one starting point’s value to 0, and reset it to -1 after it stopped running, which solved this problem nicely.
Now, I ran into another issue. My DFS function would run a BFS for a starting point, then would check all paths from there. It would continue to the next layer if the path did not overlap with existing paths (stored in an array of vectors paths). The bad paths were taking up space and wasting time. So instead of that I filled in -1 on the grid for all the squares on the path to make them occupied, so that when I ran the BFS there would only be valid paths. Here is my DFS function:
void dfs (int x, int fill) {
if (x == k) {
if (fill == sz) {
for (int i = 0; i < k; i++) {
path j = paths[i][ans[i]];
for (pair<int, int> pos : j.coords)
cout << pos.first << ' ' << pos.second << endl;
cout << endl;
}
exit(0);
}
return;
}
bfs(x);
for (int i = 0; i <= paths[x].size(); i++) {
ans.push_back(i);
path P = paths[x][i];
for (pair<int, int> j : P.coords)
grid[j.first][j.second] = -1;
dfs(x + 1, fill + P.sz);
for (pair<int, int> j : P.coords)
grid[j.first][j.second] = original[j.first][j.second];
ans.pop_back();
}
}A Simple Optimisation
All the code was done now, but the program was running extremely slowly. To speed things up, in line 15 of the DFS function, instead of searching paths from shortest to longest, I went in reverse order, which speed it up by over 5 times on average. The intuition for this is that longer paths are more likely to be longer than shorter, as most of the levels a person would be stuck on would be larger ones. Now, just adding some user input and output, and we were finished!
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n, m, k, sz, original[20][20], grid[20][20], start[10][2];
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
vector<int> ans;
struct path {
int sz;
vector<pair<int, int> > coords;
};
vector<path> paths[10];
void bfs (int x) {
grid[start[x][0]][start[x][1]] = 0;
paths[x].clear();
queue<path> q;
path init;
init.sz = 1, init.coords.push_back(make_pair(start[x][0], start[x][1]));
q.push(init);
while (!q.empty()) {
path cur = q.front();
q.pop();
paths[x].push_back(cur);
pair<int, int> pos = cur.coords.back();
for (int i = 0; i < 4; i++) {
int nx = pos.first + dx[i], ny = pos.second + dy[i];
pair<int, int> npos = make_pair(nx, ny);
if (nx < 0 || ny < 0 || nx >= n || ny >= m) continue;
if (grid[nx][ny] < grid[pos.first][pos.second]) continue;
bool flag = true;
for (pair<int, int> j : cur.coords) if (j == npos) flag = false;
if (!flag) continue;
path nw = cur;
nw.coords.push_back(npos), nw.sz++;
q.push(nw);
}
}
grid[start[x][0]][start[x][1]] = -1;
}
void dfs (int x, int fill) {
if (x == k) {
if (fill == sz) {
for (int i = 0; i < k; i++) {
path j = paths[i][ans[i]];
for (pair<int, int> pos : j.coords)
cout << pos.first << ' ' << pos.second << endl;
cout << endl;
}
exit(0);
}
return;
}
bfs(x);
for (int i = paths[x].size() - 1; i >= 0; i--) {
ans.push_back(i);
path P = paths[x][i];
for (pair<int, int> j : P.coords)
grid[j.first][j.second] = -1;
dfs(x + 1, fill + P.sz);
for (pair<int, int> j : P.coords)
grid[j.first][j.second] = original[j.first][j.second];
ans.pop_back();
}
}
int main() {
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
cin >> n >> m >> k >> sz;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++) {
cin >> original[i][j];
grid[i][j] = original[i][j];
}
for (int i = 0; i < k; i++) cin >> start[i][0] >> start[i][1];
dfs(0, 0);
return 0;
}Any optimisations would be much appreciated.
Update July 11th: I have beat the game! Work smarter not harder 🙂