I was in DT a few weeks ago and we were doing 3D modelling in SpaceClaim and then 3D printing our model. I wanted to print a regular icosahedron. It was a definite challenge, and the events that followed were not what I . . . anticipated.
First, to those who do not know what an icosahedron is, it’s my favourite among the 5 Platonic solids. To those that do not know what a Platonic solid is, it’s a polyhedron that is:
- Convex,
- Has faces that are congruent regular polygons,
- A same amount of faces meeting at each vertex.
They are also known as regular solids. Only 5 of them exist, and they are the following:




Images from: Platonic solid – Wikipedia
As you can see, the icosahedron can be a tricky shape to tackle, unlike some cubes I could mention. But really, all you need is some Pythagoras, the cosine rule, and lots of 3D imagination. Luckily, I’ve always been good at visualising things in an imaginary 3D space and maneuvering around in there. Unluckily, I still managed to fumble my calculations and ended up with a squashed icosahedron. Doing what absolutely everyone would do in this situation, I went home and pulled up my trusty whiteboard and pen. This lead me to some interesting results which I’m going to share here.
Lengths – first steps
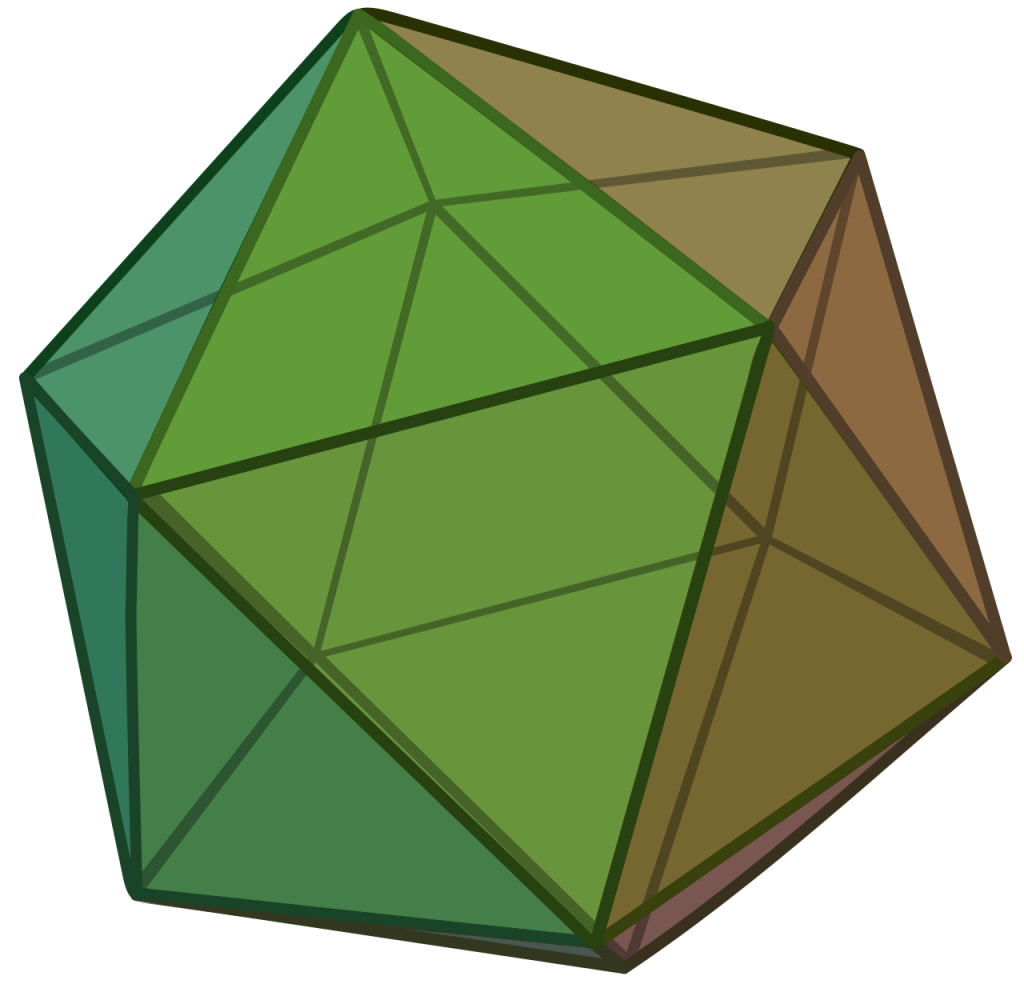
To begin with, let’s grant our icosahedron a side length of 1. Sensible enough. Now, if you look at the image of the icosahedron, there are actually many many pentagons hidden within the network of edges, all of them congruent. Let’s work out the “radius” of each pentagon, the distance from its centre to one of its vertices. We can imagine slicing the pentagon into five isosceles triangles. The triangle’s base is 1, the angle opposite of it is \(\frac{360}{5} = 72º\), and the other two edges are each length r.

Using the cosine rule, and googling the exact value of cos72, we have:
\(1^2 = 2r^2(1 – cos72)\)
\(r^2 = \frac{1}{2(1 – cos72)}\)
\( = \frac{1}{2(1 – \frac{\sqrt{5} – 1}{4})} = \frac{1}{2(\frac{5 – \sqrt{5}}{4})}\)
\(= \frac{1}{\frac{5 – \sqrt{5}}{2}} = \frac{2}{5 – \sqrt{5}} = \frac{5 + \sqrt{5}}{10}\)
I’ve left it, and all future numbers, squared for now, as when using the Pytho power and the Cosine rule everything is squared, so I won’t have to square it back later.
Height of cap
Now we turn to working out the height of the “cap” of the icosahedron. As we’ve worked out the “radius of the pentagon, we can just use Pythagoras. I’m calling the height of the cap \(h_c\) as there is also another height I want to work out later. Here we go:
\(\frac{5 + \sqrt{5}}{10} + h_c^2 = 1\)
\(h_c^2 = \frac{5 – \sqrt{5}}{10}\)
Height of Middle Section
If we cut off two caps opposite each other, we are left with a sort of rotated pentagonal prism, and I wanted the height of that. This was the bit where I got the math wrong. The key is to imagine a copy of the top face becoming a ghost and travelling down so that it’s on the same level as the bottom face. Now, the bottom face becomes a sort of 10-pointed star, like this:

Why does this come in useful? Well, there is a very sneaky right-angled triangle in our solid that we can exploit to find the height. The hypotenuse is an edge that does not belong to the two pentagonal faces. The two other sides are the height of the shape, and the distance between two adjacent tips of the star shape I showed just now. Here’s another picture to show you the triangle I’m describing:

We know the hypotenuse is 1, and we can work out the shorter leg, so using Pythagoras we can work out the height! Let’s work out the short side first. It’s part of an isosceles triangle with two edges being radii of the circle, which we’ve worked out, and an included angle of 36º, so we bring in the Cosine Rule:
\(a^2 = b^2 + c^2 – 2bc\cdot cosA\)
As \(b = c, a^2 = 2b^2 – 2b^2\cdot cos36º\)
\(a^2 = 2\cdot \frac{5 + \sqrt{5}}{10} \cdot (1 – \frac{1 + \sqrt{5}}{4})\)
\(a^2 = \frac{5 + \sqrt{5}}{5} \cdot \frac{3 – \sqrt{5}}{4}\)
\(= \frac{5 – \sqrt{5}}{10}.\)
Now that we know the length of the red base, as the hypotenuse is one of the sides of the icosahedron, that is, 1, we can just use Pytho Power to figure out the height of the middle band, \(h_m\):
\(h_m^2 + a^2 = 1\)
\(h_m^2 = 1 – \frac{5 – \sqrt{5}}{10}\)
\(= \frac{5 + \sqrt{5}}{10}.\)
Nice! Now, with all the measurements of the ‘radius’ of the pentagon and the height of the cap and the middle, we can finally make the icosahedron. And the happy result, created in the final DT lesson this year.


Bonus math!
Let’s find the surface area and volume of an icosahedron given its side length. The surface area is simple enough, just 20 equilateral triangles. For this unit icosahedron, the surface area is \(20 \times \frac{\sqrt{3}}{4} = 5\sqrt{3}\) square units, and for an icosahedron of side length s, the surface area is \(5\sqrt{3}s^2\).
The volume is a little trickier. We can imagine slicing the icosahedron into 20 identical tetrahedrons, or triangular pyramids. The base of one of these is just a face of the icosahedron, while the height is the distance from the centre of the icosahedron to the centre of the triangle. The formula for the volume of a pyramid involves finding its height, so let’s try to do that.



From the images above, we can hopefully see that we can use yet more creative Pytho Power to find the height of the tetrahedron. First, by using it to find the radius of the ‘circumsphere’ of the icosahedron which is the length of one of the edges. Then, some trig to find the distance from the centre to a corner of the equilateral triangle base. Then, use more Pytho Power to find the height of the tetrahedron \(h_t\).
\(R^2 = r^2 + \frac{h_m^2}{4}\)
\(= \frac{5 + \sqrt{5}}{10} + \frac{5 + \sqrt{5}}{40}\)
\(= \frac{25 + 5\sqrt{5}}{40} = \frac{5 + \sqrt{5}}{8}\)
Next, the distance from the centre of the equilateral triangle to a corner is \(\frac{\sqrt{3}}{3}\). Now,
\(h_t^2 = \frac{5 + \sqrt{5}}{8} – \frac{1}{3}\)
\(= \frac{15 + 3\sqrt{5} – 8}{24}\)
\(= \frac{7 + 3\sqrt{5}}{24}\)
\(h_t = \frac{\sqrt{6(7 + 3\sqrt{5})}}{12}\)
What an absolutely ridiculous and ugly thing. Hopefully we can manage to simplify it out later, actually, now! We have all the values we need to work out the volume of the icosahedron. Here we go!
\(20 \cdot \frac{1}{3} \cdot \frac{\sqrt{3}}{4} \cdot \frac{\sqrt{6(7 + 3\sqrt{5})}}{12}\)
\(= \frac{5\sqrt{3}}{3} \cdot \frac{\sqrt{6(7 + 3\sqrt{5})}}{12}\)
\(= \frac{5\sqrt{18(7 + 3\sqrt{5})}}{36}\)
\(= \frac{5\sqrt{2(7 + 3\sqrt{5})}}{12} = \frac{5\sqrt{14 + 6\sqrt{5}}}{12}\)
Dealing with those pesky square roots should be the final step to the volume hunt! Let’s isolate it on it’s on so it doesn’t look that scary:
\(\sqrt{14 + 6\sqrt{5}}\)
We can guess (or try the hypothesis, if ‘guess’ makes you uncomfortable) that the form of the simplification is \(a + b\sqrt{5}.\) Squaring that gives \(a^2 + 5b^2 + 2ab\sqrt{5}\). So, we have the simultaneous equations of \(a^2 + 5b^2 = 14\) and $ab = 3$. After substituting \(b = \frac{3}{a}\) or just by trial and error, we find that \(a = 3, b = 1\). Now back to the entire thing.
\(\frac{5\sqrt{14 + 6\sqrt{5}}}{12} = \frac{5(3 + \sqrt{5})}{12}\)
\(= \frac{15 + 5\sqrt{5}}{12}.\)

