The Catalan numbers are a sequence of numbers that appear in a large number of counting problems involving recursion. They are named after the French-Belgian mathematician Eugène Charles Catalan (1814-1894) and begin thus:
\(1, 1, 2, 5, 14, 42, \cdots\)
Introduction problem
In how many ways can 10 distinct people seated at a round table shake hands (in pairs) so that no handshakes cross? An example is shown below:
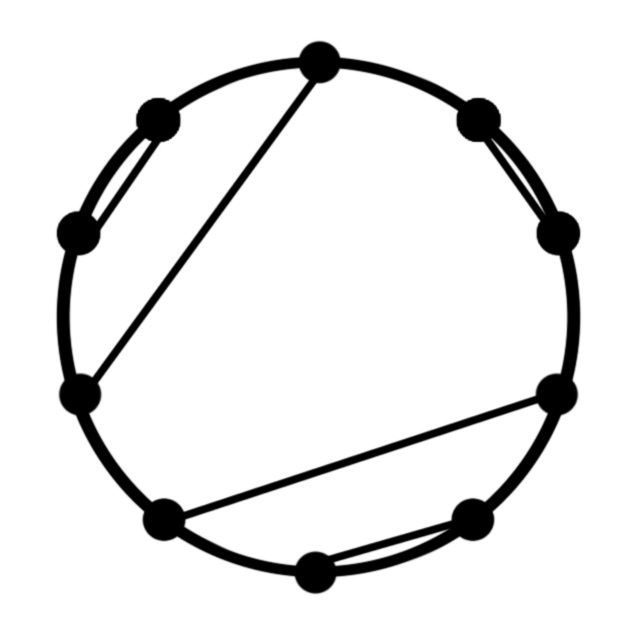
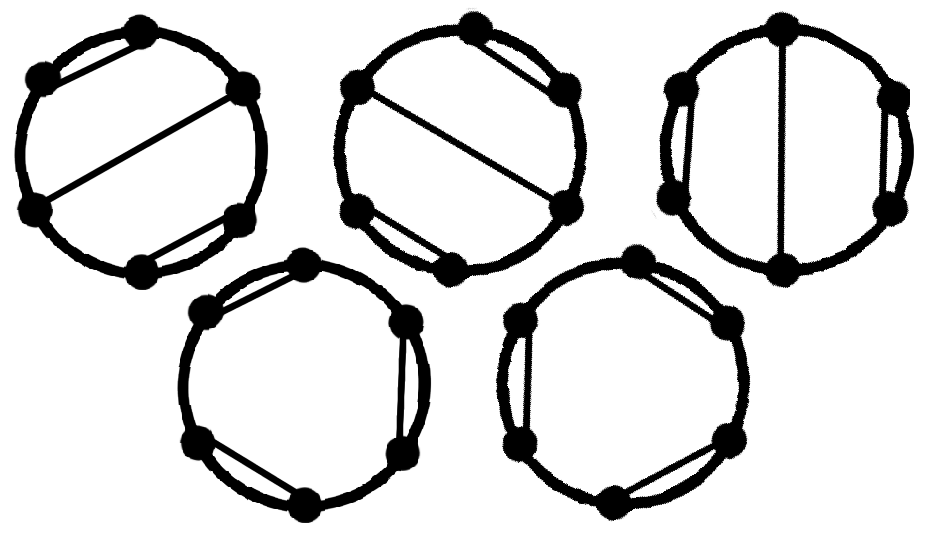
Well, how to start? Let’s first look at some smaller cases, say, with 2, 4, and 6 people, and let’s define \(H_n\) as the number of arrangements for 2n people. Obviously, $latexH_1 = 1.$ Next, \(H_2 = 2\), because if we arrange the people in a square, the handshakes can either go across the vertical edges or the horizontal ones. There are a few more for \(H_3\), so I’ll put a picture of all the arrangements instead:
The Catalan Recurrence
Let’s now compute \(H_4\). But not so fast! Let’s draw our possibilities for the first choice and see what happens.
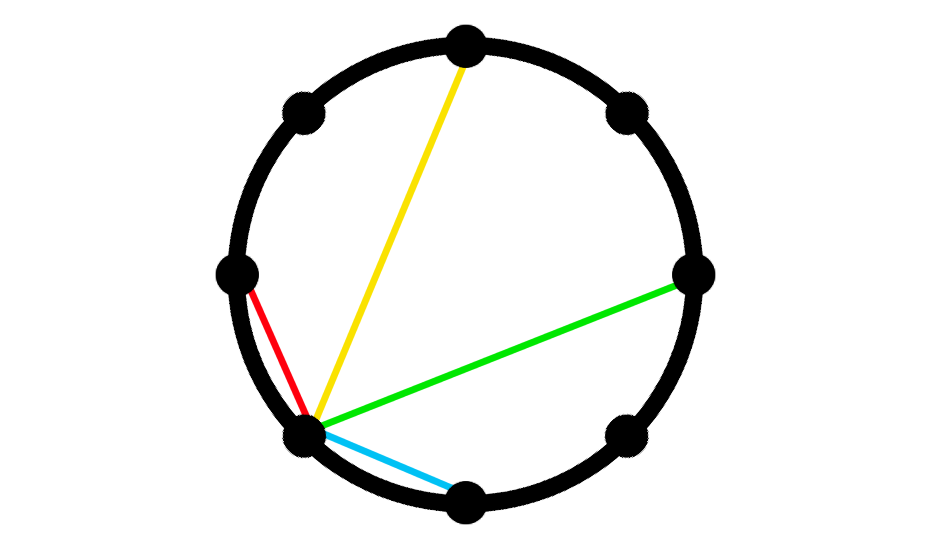
If we choose the red line as our first handshake, we have 6 people remaining on one side, and we have \(H_3\) ways of organising them. If we choose the yellow line, there’s 2 people on one side, and 4 people on the other, which means there’s \(H_1H_2\) arrangements. Continuing like this, we find the recurrence
\(H_n = \sum_{k = 0}^{n – 1} H_k H_{n – k – 1}.\)
What are these numbers? You guessed it, this is the recurrence for the Catalan numbers. If we see another problem with this recurrence, we’ll know that the solutions are the Catalan numbers.
Another Catalan Problem
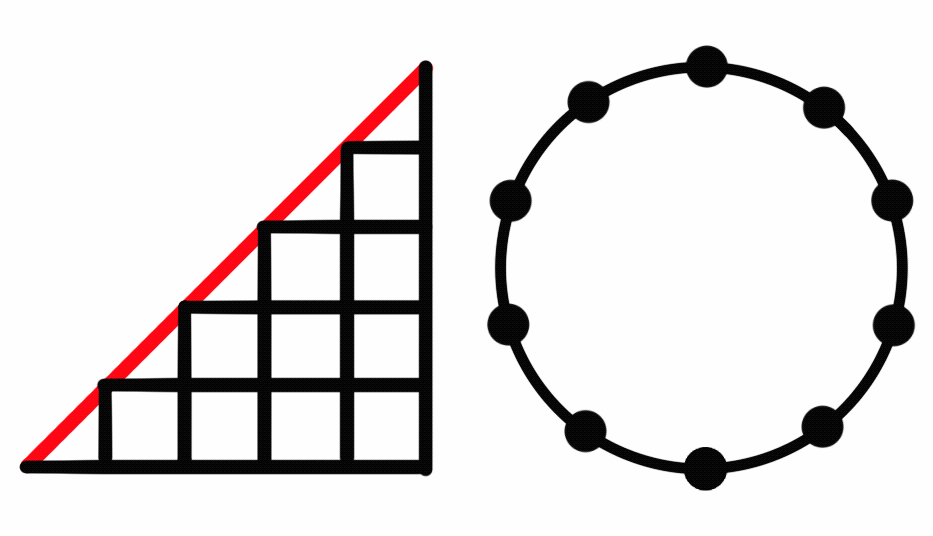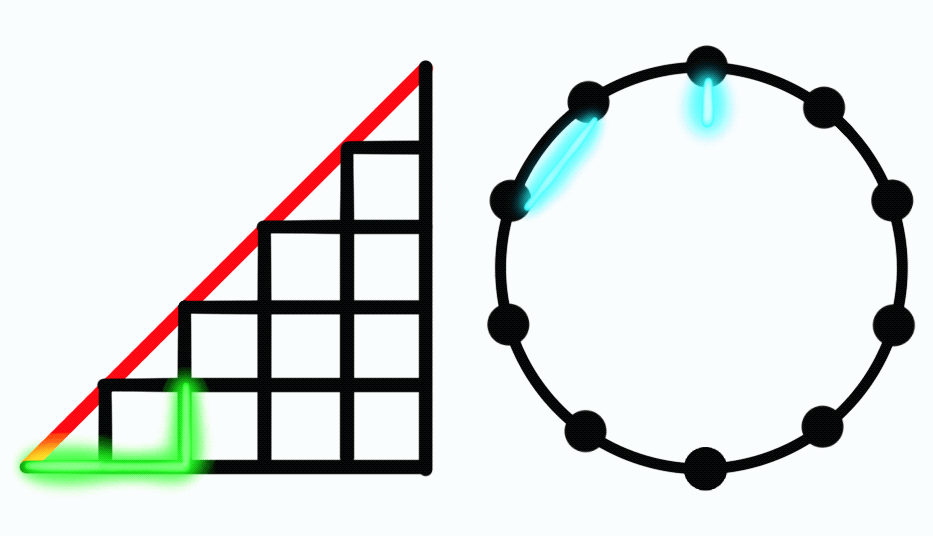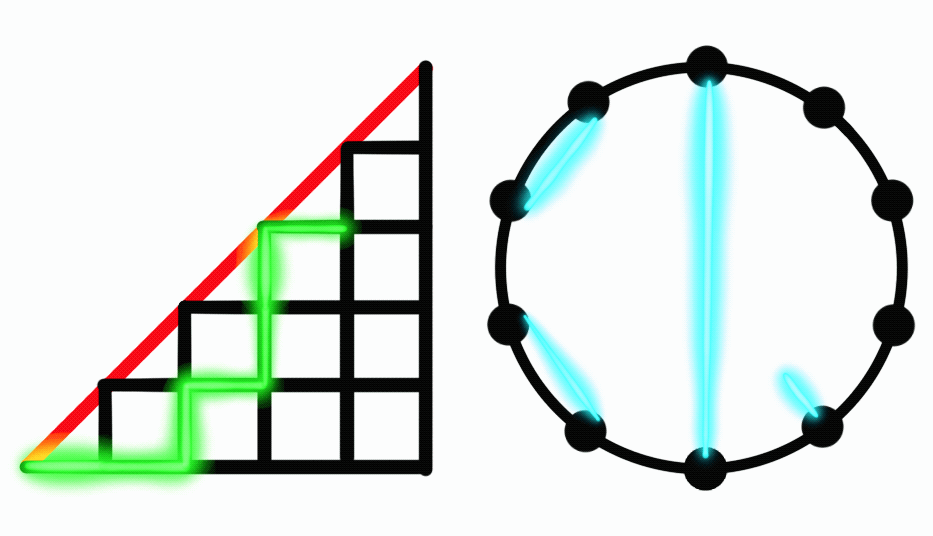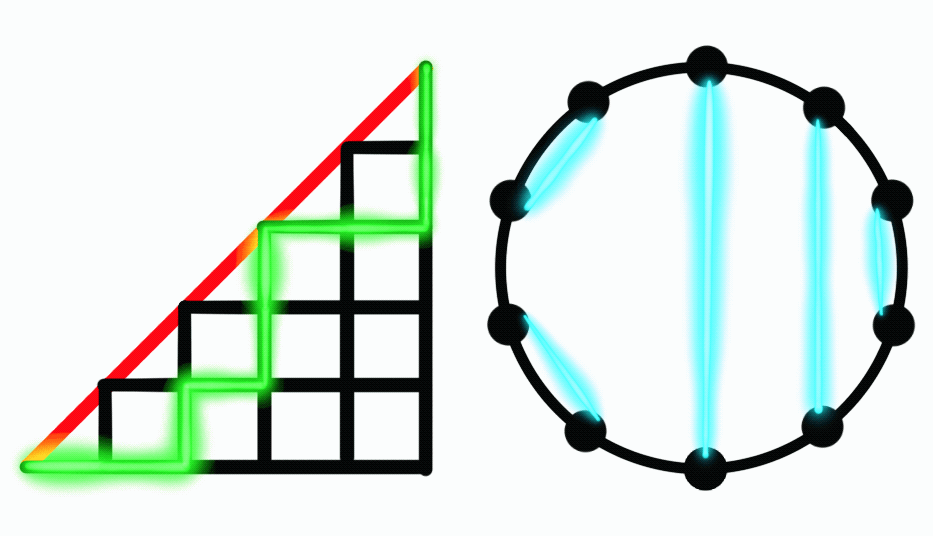
How many ways are there to travel from (0, 0) to (n, n) by moving 1 unit right wards or upwards while not being above over the line \(y = x\)? If you want to try this yourself, which I highly recommend, try find a pattern between the number of paths \(P_n\) and the handshakes \(H_n\).

One-to-one correspondence with handshakes
The first way we’re going to look at this is to compare it to the handshakes. At each point, we have two things we can do: move up or move to the right. For each person at the table in, say, a clockwise direction, that person can either extend a hand for someone to shake or shake the first extended hand going anticlockwise. In our second case, there must never be more people accepting a handshake than offering a handshake. This is the same as not having a greater y-value than x-value, which is what our question wants. Therefore, there’s a one-to-one correspondence with each seating plan and path, and the answer to our question is also the Catalan numbers!
A Closed Form?
We’ve seen the recurrence relationship for the Catalan numbers, but is there an actual closed-form formula? To find one requires a very sneaky trick. We’re going to use complementary counting(not the trick): finding the total number of paths and subtracting the ones we don’t want. The first value is quite straightforward: as we take \(2n\) steps and \(n\) of them are to the right, there are \(C^{2n}_n\) paths we can choose. Finding the number of unwanted paths requires an ingenious trick: as soon as we go over the red line, we invert our steps. Observe!
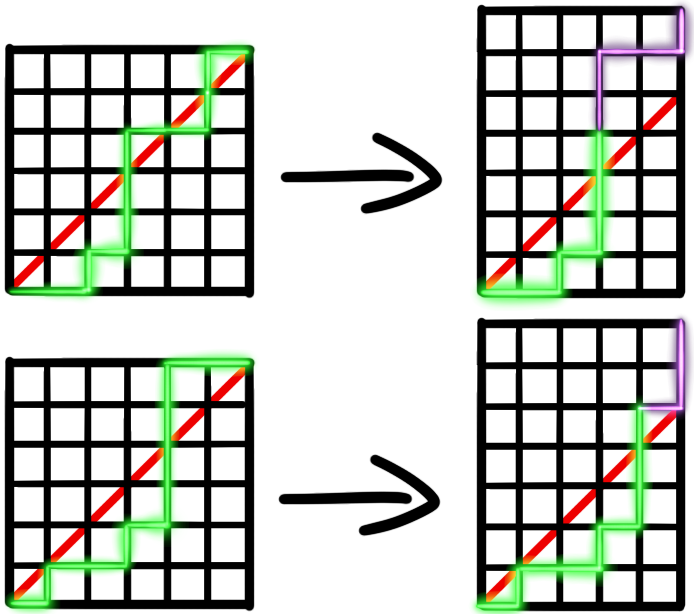
As you can see, the purple path always encloses a \(k \times (k + 1)\) rectangle, so after we flip our path we get an \((n – 1) \times (n + 1)\) rectangle, where \(n + 1\) of the \(2n\) moves are up. Therefore, there’s a one-to-one correspondence with all the paths that go above the line with all the paths in a \((n – 1) \times (n + 1)\) rectangle, so our closed form is:
\(\Large{C^{2n}_n – C^{2n}_{n + 1}}\)
\( \Large{\frac{(2n)!}{n!n!} – \frac{(2n)!}{(n + 1)!(n – 1)!}}\)
\(=\Large{\frac{(2n)!}{n!n!} – \frac{(2n)!\cdot n}{(n + 1)n! \cdot n!}}\)
\(=\Large{\frac{1}{n + 1} \cdot \frac{(2n)!}{n!n!}}\)
\(= \Large{\frac{C^{2n}_n}{n + 1}}.\)
The end
\(\binom{n}{r}\)